2016년 3월, 세계적으로 큰 이슈를 몰고 온 게임이 성사되었습니다. 그것은 바로 세계 최고 바둑기사인 대한민국의 이세돌과 구글 딥마인드의 인공지능 바둑 프로그램 알파고(alphago)와의 대결인 ‘구글 딥마인드 챌린지 매치(Google DeepMind Challenge Match)’였는데요. 그 결과는 여러분들도 아시다시피 4:1의 스코어로 알파고가 압승을 거두게 됩니다. 이는 우리 모두에게 매우 충격적인 소식이었습니다.
1997년 IBM에서 만든 인공지능 ‘딥 블루(Deep Blue)’가 체스 세계 챔피언을 이겼을 때, 뉴욕 타임스는 바둑에서 컴퓨터가 사람을 이기기 위해서는 100년 이상이 걸릴지도 모른다고 보도했었습니다.

실제로 딥 블루는 체스 게임에서 상대 말이 움직이는 경우의 수를 모두 탐색해 상대방이 이길 수 있는 가장 적은 수를 택하는 방식입니다. 하지만, 바둑의 경우 체스와는 달리 딥 블루의 방식으로 계산할 수 없을 만큼의 어마어마한 경우의 수를 가진 말의 움직임이 존재합니다.
전문가들은 바둑에서는 어떤 경우든 우주 전체의 원자 수보다 더 많은 조합의 경우의 수가 존재한다고 합니다. 따라서 모든 경우의 수를 계산하여 바둑을 둔다는 것은 아무리 ICT 기술이 발전한다 해도 현실적으로 불가능하다는 것이 다수 학자의 정설이었지요.
그런데 불과 약 20년이 흐른 뒤에 알파고라는 바둑프로그램은 세계 최고의 바둑기사를 상대로 압승을 거두었습니다. 이는 단지 우연이었을까요? 이세돌과의 대결 이후 알파고는 10개월에 걸쳐 더욱 진화했고, 2016년 12월 29일부터 지난 1월 4일까지 인터넷 바둑사이트 2곳에서 세계 최고수들과 총 60판의 바둑을 둬서 한 판도 지지 않고 전부 다 승리를 거두었다고 합니다. (한국랭킹 1위 박정환 9단 상대5전 전승, 중국랭킹 1위 커제 9단 상대3전 3승 포함)

그렇다면 알파고는 어떠한 방식으로 상대를 제압하는 바둑을 두는 것일까요? 구글 개발팀에 의하면 알파고는 몬테카를로 알고리즘에 딥러닝(Deep Learning) 알고리즘을 결합하여 스스로 학습하는 방식을 택한다고 합니다. 여기서 스스로 학습하는 방식을 머신러닝(Machine Learning)이라고 일컬으며, 딥러닝 알고리즘은 인공신경망(Artificial Neural Network; ANN) 알고리즘을 기반으로 하는 예측 알고리즘이라고 말할 수 있습니다.
따라서 알파고는 기본적으로 인공신경망 기반의 인공지능 컴퓨터라고 할 수 있겠죠. 이러한 점에 착안하여 이번 시간에는 알파고의 기반이 되는 알고리즘인 인공신경망에 대해서 간단히 알아보겠습니다.
인공신경망이란?
인공신경망은 생물학의 신경망에서 영감을 얻은 학습 알고리즘입니다. 시냅스의 결합으로 네트워크를 형성한 인공 뉴런이 학습을 통해 시냅스의 결합 세기를 변화시켜 문제해결능력을 가지는 비선형 모델이라고 설명할 수 있겠습니다.
1940년대 중반에 임계 논리(threshold logic)라 불리는 알고리즘을 바탕으로 신경망을 위한 수학적 모델이 제안되었습니다. 이후 1980년대 중반 데이비드 럼멜하트(David E. Rumelhart)와 제임스 맥클레랜드(James McClelland)가 연결주의(connectionism)로 대변되는 병렬분산처리 측면에서 인공신경망을 기술한 이후 최근까지 다양한 분야에서 활발하게 연구되고 있는 알고리즘입니다.
일반적으로 사용되는 기본적인 인공신경망 알고리즘인 다층인공신경망(multi-layer neural network)의 경우 아래 그림과 같이 입력층(input layer), 은닉층(hidden layer), 그리고 출력층(output layer),이렇게 세가지 층으로 구분이 됩니다. 그리고 각 층들은 노드들로 구성되어 있습니다. 아래 그림의 예에서는 입력층은 4개의 노드, 은닉층은 3개의 노드, 그리고 출력층은 1개의 노드를 가지고 있습니다.
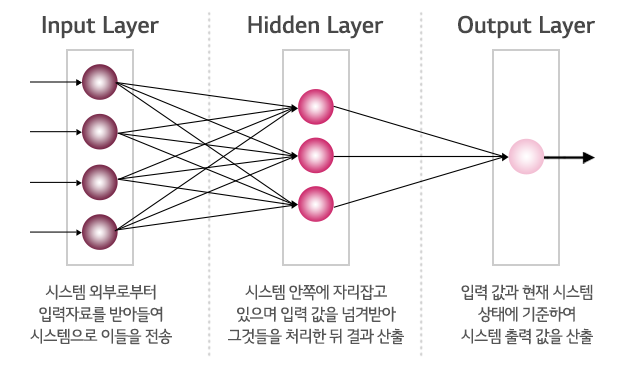
입력층은 예측값(출력변수)을 도출하기 위한 예측변수(입력변수)의 값들을 입력하는 역할을 합니다. 만약 n개의 입력 값들이 있다면 입력층은 n개의 노드를 가지게 됩니다. 은닉층은 모든 입력노드부터 입력값을 받아 가중합을 계산하고, 이 값을 전이함수에 적용하여 출력층에 전달하게 됩니다. 각 입력노드와 은닉노드들은 모두 가중치를 가지는 망으로 연결되어 있으며 은닉노드와 출력노드도 마찬가지로 연결되어 있습니다.
이 가중치는 연결강도로 표현되며 랜덤으로 초기에 주어졌다가 예측 값을 가장 잘 맞추는 값으로 조정되게 됩니다. 전이함수는 비선형함수를 사용하게 되며, 이러한 전이함수를 통하여 출력층에 예측 값이 전달되기 때문에 인공신경망이 비선형 모델로서 역할을 할 수 있게 됩니다.
예를 들어, 0.2와 0.9 두 개의 입력 값으로 0.5라는 예측값을 도출하는 인공신경망 모델을 학습시키는 과정을 생각해보겠습니다. 아래 그림과 같이 입력층에는 2개의 노드가 할당되며 출력 층에는 1개의 노드가 할당됩니다. 그리고 은닉층은 1개이며, 은닉노드는 3개로 임의로 설정합니다. 여기서 은닉층과 은닉노드의 개수는 다수의 반복실험을 통해 사용자가 적절하게 설정해야 하는 값입니다.
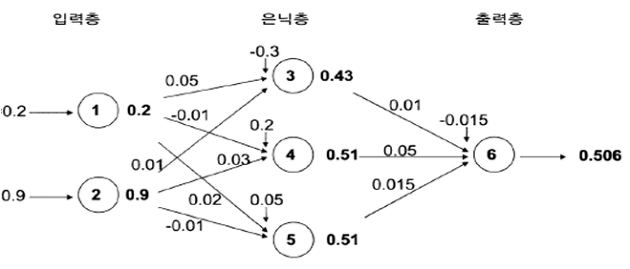
위 그림에서 은닉층 첫번째 노드인 노드3의 할당 값인 0.43이 나오는 과정을 간단히 살펴보겠습니다. 각 노드와 노드의 연결강도는 초기에 무작위로 할당되며, 정확한 예측값 도출을 목표로 최적값을 찾아가게 됩니다. 위 그림에서 노드 1에서 노드3으로의 연결강도는 0.05, 노드 2에서 노드 3으로의 연결강도는 0.01이 됩니다. 그리고 노드3 앞에 할당된 -0.3은 편의 값(bias)으로써 이 또한 초기에 무작위로 할당되게 됩니다.
이러한 과정들이 굉장히 복잡하다고 생각되지만, 이 모든 과정이 인간의 뇌에서 작동되는 원리를 수학적 모델로 가져온 것임을 알아두시기 바랍니다. 노드 3에서 수행되는 가중합 연산과정은 [-0.3(노드3의 bias) + {0.2(노드1의 입력값)Ⅹ 0.05(노드1에서 노드3으로의 연결강도)} + {0.9(노드2의 입력값) Ⅹ 0.01(노드2에서 노드3으로의 연결강도)}] 로 표현할 수 있습니다. 이렇게 도출된 가중합을1/(1+e^(-x) )라는 전이함수에 적용하면 1/(1+e^(-[-0.3+(0.2)(0.05)+(0.9)(0.01) ] ) ) = 0.43 이라는 노드3의 최종값이 계산됩니다.

이러한 계산과정을 거쳐 최종적으로 출력 노드인 노드5의 값은 0.506이 산출되는데요. 목표값인 0.5와 가장 가까운 값이 도출될 때까지 반복 수행되며, 연결강도와 편의 값들이 수정되게 됩니다. 여기서 재미있는 점은 만약 이러한 인공신경망 모델에서 은닉층이 사라지고 가중합의 전이함수로의 적용이 없다면 대표적인 통계모형인 회귀모델과 같은 알고리즘이 도출된다고 할 수 있습니다.
딥러닝과 인공신경망, 인공지능의 발전은 어디까지 가능할까?
지금까지 기본적인 인공신경망 알고리즘이 학습하는 과정을 간단하게 살펴보았습니다. 인공신경망은 기존의 분류 혹은 예측모형보다 복잡한 모델을 가지고 있으며 많은 계산량을 요구하는데요. 실제로 다양한 분야에서 우수한 성과를 보여줌으로써 그 유용성을 인정받고 있습니다. 그러나 이러한 인공신경망은 커다란 하나의 문제점을 가지고 있습니다.
연결강도, 은닉층의 수와 같은 다양한 파라미터들을 최적값으로 수렴시키는 과정에서 인공신경망 모델이 학습데이터에 과적합되는 경향을 보인다는 것입니다. 이는 학습된 모델을 새로운 데이터에 적용했을 경우 성과가 떨어진다는 의미입니다. 지금까지 실증적으로 그 유용성을 인정받은 인공신경망은 많은 학자에 의해 과적합 문제를 해결하기 위한 많은 노력이 있었습니다. 그러나, 그 효과성이 미미했습니다.
최근 알파고가 도입하고 있는 딥러닝이라는 알고리즘이 인공신경망의 과적합 문제를 해결할 수 있는 강력한 대안으로 떠오르며, 다시 한번 인공신경망이 전 세계적으로 주목을 받고 있습니다. 머신러닝을 통한 인공지능의 발전이 어디까지 가능할지 그 무한한 가능성이 기대됩니다.
글ㅣ 안재준 교수ㅣ 연세대학교 정보통계학과


